Integración
Integral indefinida
Sean F(x) f(x) dos funciones reales de variable real,
definidas en un intervalo I o en todo el campo de los números reales, se tiene
que la función F(x) es una primitiva de la función f(x) si la derivada F'(x) es
igual a la función f(x), para toda variable perteneciente al intervalo.
Por ejemplo, la función F(x)= 2x4 es una primitiva de la función f(x)= 8x3 pues
al derivar la primera tenemos que se obtiene la función original f(x)= 8x3.
Si la función F(x) es una primitiva de la función original f(x), la primitiva F(x) + k (una constante) también es primitiva de la función original para todo número perteneciente a los números reales. De esto se desprende que si conocemos una primitiva de una función podemos obtener otras primitivas al sumar diferentes constantes.
Si la función F(x) es una primitiva de la función original f(x), la primitiva F(x) + k (una constante) también es primitiva de la función original para todo número perteneciente a los números reales. De esto se desprende que si conocemos una primitiva de una función podemos obtener otras primitivas al sumar diferentes constantes.
Si tenemos f(x) una
función real de variable real, al conjunto de todas las primitivas de esa
función se llama integral indefinida de la función, y se lee integral
indefinida de la función f(x) respecto a
dx o también integral de f de x diferencial de x.
La transformación que permite calcular la función primitiva
de otra función se llama integración.
Para calcular la integral indefinida de una función exponencial, sumamos una unidad al exponente n y el resultado lo tomamos además como denominador de la nueva expresión, sumando una constante C a toda la expresión anterior cuando la integral es indefinida. (El valor de n debe ser distinto de -1)
En la gráfica tenemos la representación de una curva en color marrón y la representación gráfica de su integración. Al aplicar la integral indefinida, que es aquella que no está acotada entre dos parámetros del eje x, tenemos que sumar una unidad al exponente del numerador, el valor del nuevo exponente lo utilizamos también como denominador, a todo ello le aumentamos una constante que puede tener cualquier valor k, ya que al derivarla genera el valor cero.
------------------------------------------------------------------------------------------------------------------------
Integral definida
Una integral definida de f(x) en el intervalo (a,b) es el área orientada de la figura limitada por la gráfica de f(x), el eje x y las rectas (a,b).
Cuando decimos que el área está orientada quiere decir que
va a depender de si la función es positiva o negativa en el intervalo ab.
Si dividimos el intervalo (a,b) en subintervalos pero de igual
amplitud, en cada intervalo menor la función alcanzará un máximo y un mínimo
absolutos, que es el mayor y menor valor de la función en el subintervalo. Si
en cada subintervalo menor se traza una recta paralela al eje x por cada máximo
absoluto y por cada mínimo absoluto, se tienen rectángulos exteriores e
interiores.
Si consideramos la suma de las áreas de todos los rectángulos
exteriores y la suma de todas las áreas de todos los rectángulos interiores, la
integral definida está comprendida entre ambos valores. Si hacemos
subdivisiones de menor amplitud, las áreas se van aproximando cada vez más y con mayor
exactitud a la integral definida, de esta manera podemos decir que
el límite cuando la amplitud tiende a cero es la integral definida entre los
intervalos de la función.
---------------------------------------------------------------
---------------------------------------------------------------
Una integral definida nos sirve para calcular áreas, aunque cualquier figura generada por líneas rectas como pueden ser los polígonos se pueden resolver fácilmente mediante expresiones sencillas, vamos a practicar unos cuantos ejemplos para comprobar el método para el cálculo de áreas. De esta manera es más fácil extrapolar la metodología a otros elementos más complejos como pueden ser las curvas y las áreas comprendidas entre ellas o entre curvas y segmentos.
En la figura integramos la ecuación de la recta para calcular el área que se produce debajo de ella entre los intervalos tres y cero. En cada uno de los términos de la ecuación sumamos una unidad al exponente y ese número lo utilizamos como denominador. Éste cálculo lo vamos a hacer entre tres y cero por tanto sustituimos en la expresión dentro de las variables el valor tres y aplicamos a continuación la diferencia de la misma expresión integrada con el valor cero, que por supuesto nos va a dar cero.
De esta manera tenemos que a sustituir el tres en la expresión en la que aplicamos la integral definida nos da el valor del área nueve unidades cuadradas.
Verificamos que esto es cierto mediante la fórmula de el área del triángulo: base por altura partido por dos, esto es, 3 × 6 igual a 18, entre 2, igual a nueve.
---------------------------------------------------------------
Otro ejemplo, para calcular el área del cuadrado definido por la recta adecuación y=2, entre dos y cero, calculamos la integral de dos, dos es lo mismo que dos por x elevado a cero, por tanto al sumarle una unidad a x elevado 0 tenemos x elevado a uno, si tomamos este exponente (uno) y lo utilizamos como denominador queda que 2x partido por uno es igual a 2x.
Debemos aplicar entonces los valores dos y cero sobre la integral, sustituyendo en la expresión:
2 × 2= 4 - 2 × 0=0, por tanto la integral definida entre cero y dos de la recta y=2 vale cuatro unidades cuadradas, el área del cuadrado que es lado por lado.
---------------------------------------------------------------
Para calcular el área del rectángulo (base por altura) de la recta horizontal de ordenada igual a tres comprendida entre los intervalos 2 y 4, aplicamos la integral de la constante tres y nos queda según el método anterior 3x, que evaluada entre 4 y 2, multiplicamos 3 × 4 y a continuación le restamos 3 × 2 y tenemos seis unidades cuadradas.
---------------------------------------------------------------
Para calcular el área comprendida entre la la recta de ecuación y= -x+2 y entre los intervalos cero y dos, integramos cada uno de los términos de la ecuación y tenemos que al elevar una unidad al exponente de la variable -x obtenemos -x al cuadrado, este exponente lo utilizamos para el denominador.
A continuación el siguiente término al integrarlo vemos que dos se transforma en 2x dividido entre uno, por tanto hay que calcular la integral entre la suma de ambos términos. Al evaluar la integral entre dos y cero, sustituimos en la variable x el número dos y obtenemos dos unidades cuadradas.
--------------------------------------------------------------------
Para calcular el área de este trapecio, tomamos la ecuación de la recta y hallamos el área comprendida entre los valores 3 y 1.
Al integrar el primer término tenemos que a 2x le sumamos una unidad al exponente y queda 2x al cuadrado, este exponente lo utilizamos también como denominador. El siguiente término le sumamos su integral y queda que tres por x elevado a cero, al sumarle una unidad al exponente queda 3x/1, es el segundo término de la expresión.
La suma de ambos términos evaluada entre 3 y 1 (extremos laterales del trapecio) genera dos expresiones de las que se calcula la diferencia, aplicando la primera el valor tres y aplicando en la siguiente el valor uno en la variable. Al aplicar la diferencia entre ambos tenemos que el área vale 14 unidades cuadradas.
--------------------------------------------------------------------
Para calcular el área comprendida entre la recta cuya expresión parece el gráfico evaluada entre -3 y -6 (líneas verticales de la figura), operamos como hasta ahora, sumamos una unidad al exponente y ese número lo utilizamos como denominador. A continuación sustituimos el -3 y el -6 en la expresión que hemos calculado y aplicamos la diferencia entre ambas. El orden que debemos seguir siempre es de derecha e izquierda, como el -3 queda más hacia la derecha, primeros sustituimos al -3 en la expresión y al calcular esto le restamos luego el -6 aplicado a la misma expresión, la diferencia de ambos elementos genera el área de la figura que es 31,5.
--------------------------------------------------------------------
Cuando calculamos el área lo que importa es el valor absoluto que es la magnitud sin tener en cuenta el signo. Es un dato a tener en cuenta ya que si el área que estamos calculando es de una figura geométrica que está por debajo del eje x, va a salir negativa.
El área definida por la recta de pendiente positiva 1/3, esto es, 0,33, y que corta al eje de las ordenadas en el punto -3, vamos a calcular obteniendo su ecuación el área que queda determinada por la recta y por las líneas verticales que pasan por el punto tres y el punto cero.
Hacemos la integral definida entre ambos elementos de ambos términos de la ecuación, por lo que tenemos que 1/3 de x pasa a estar elevado al cuadrado y dividido todo por dos, ya a la variable del numerador se le suma una unidad y un nº igual al exponente pasa al denominador. El siguiente término de la expresión de la recta es -3, al integrarlo se transforma en -3x.
Al aplicar la diferencia entre ambos términos y sustituyendo el tres en las variables tenemos que el área es -7,5 unidades cuadradas, cuyo valor absoluto es la magnitud 7,5 unidades cuadrada.
--------------------------------------------------------------------
En la figura podemos observar la función cuya ecuación aparece en color rojo y cuya representación gráfica es la curva también de color roja. Vamos a calcular el área comprendida entre el punto 0 y el punto -1. Como podemos observar esta comprendido este tramo debajo del eje x, por tanto su valor va a salir negativo.
Para calcular la integral de x a la cuarta más x al cubo entre 0 y -1, sumamos una unidad a cada exponente de los términos y ese mismo número también lo tomamos como denominador en cada uno de los términos. Por tanto x a la cuarta se transforma en x a la quinta partido por cinco más el siguiente término, x al cubo se transforma en x a la cuarta partido por cuatro, a continuación sacamos factor común y queda x a la cuarta que multiplica a (4x+5), todo ello dividido por 20, tras aplicar el mínimo común múltiplo. Esto es lo que aparece en la expresión superior en color verde, inmediatamente debajo hemos sustituido el cero en toda la expresión y le hemos restado la misma expresión, pero sustituyendo la variable x por -1. Si operamos nos queda -1 dividido entre 20 y el cociente de esto es el área de la figura, en valor absoluto 0,05 unidades cuadradas.
--------------------------------------------------------------------
Si queremos calcular el área del triángulo ABC, integramos el segundo miembro de la ecuación de la recta entre los puntos BA de coordenadas 0 y -1, que son los que determinan el intervalo correspondiente al área.
Al sumar una unidad al exponente y dividir el término por ese mismo exponente, obtenemos la primera expresión que hay que evaluar desde 0 y -1. Sustituyendo el cero en las variables tenemos que el resultado de la primera expresión es cero menos la segunda expresión en la que sustituimos ser -1 tenemos como resultado -2,5 unidades cuadradas. Es negativo por estar debajo del eje de las abscisas.
--------------------------------------------------------------------
Para calcular el área de la figura, podemos hacer su representación y ver que es simétrica central respecto al centro C. Por tanto es suficiente con que calculemos el área de uno de los dos triángulos, multiplicándolo luego por dos para obtener el área total.
Calculamos el área comprendida entre la recta dada y la recta y= 0, todo ello entre el intervalo 0 y -1.
Sumando una unidad al exponente de la variable y tomando ese nuevo valor del exponente como denominador tenemos la integral en la que sustituimos en las variables los valores del intervalo 0, -1.
Obtenemos por tanto un valor negativo por estar debajo del eje x, pero tomamos su valor absoluto -1,5- y lo multiplicamos por dos obteniendo el área total de la figura, que es tres.
--------------------------------------------------------------------
Ejercicio parecido al anterior pero como los triángulos son de distinto tamaño, aplicamos la integral definida entre 4 y 2 y a continuación le sumamos el valor de la integral entre 2 y 1.
Operando como siempre, sumando una unidad al exponente de la variable y considerando este nuevo número como denominador. Sustituyendo a continuación los valores 4 y 2 para la primera área y 2 y 1 para la siguiente obtenemos el valor absoluto de -2 + 0,5, por lo que tenemos de área 2,5 unidades cuadradas.
--------------------------------------------------------------------
En la figura tenemos la ecuación de una recta y=2x-2, es una recta que tiene pendiente 2 ( numero que está al lado de x) y que corta al eje vertical en el punto -2.
Sustituimos en la ecuación y por cero, ya que cuando y vale cero tenemos que la recta corta al eje x en un punto, para calcular este punto despejamos y tenemos que x es igual a uno.
Para calcular el área debajo de la recta entre el límite tres y la intersección con el eje x, ( punto uno) evaluamos la función entre ambos términos sustituyéndolos en la integral de la ecuación, al primer termino se le suma una unidad al exponente y obtenemos 2x al cuadrado partido 2.
A continuación le restamos el segundo término, que es una constante 2 (se puede entender 2. x elevado a cero -esto es, dos por uno-), elevando una unidad al exponente de esta variable obtenemos 2x partido por uno, por tanto tenemos que su integral es 2x.
Sustituyendo en la expresión el tres y a continuación el uno y aplicando la diferencia entre ambas tenemos que el área de la figura es 4 unidades cuadradas.
--------------------------------------------------------------------
Dada la recta cuya ecuación es y igual a dos, determinar el área de la figura comprendida entre las rectas verticales que pasan por el 2 y por el 5 y por el eje x.
Hacemos la integral de dos entre los dos intervalos, 5 y 2.
La integral de dos es 2x elevado a uno dividido entre uno, esto es, 2x.
sustituimos el 5 una variable de 2x y le restamos al sustituir el dos de la variable 2x, quedando 10 - 4=6
-----------------------------------------------------------
Igual que el ejercicio anterior, tenemos la misma recta evaluada entre 4 y -3. Sustituyendo ambos números en la resolución de la integral obtenemos de área 14 unidades cuadradas
-------------------------------------------------
Ejercicio igual al anterior entre -3 y -5. Sustituyendo ambos números en la resolución de la integral obtenemos el área de cuatro unidades cuadradas.
----------------------------------------------
Para calcular el área de la parábola comprendida entre el número dos y el cero, calculamos la integral sumando una unidad al exponente y tomando ese mismo número como denominador, a continuación incluimos en la variable el punto dos, ya que el área va a estar comprendida entre el dos y el cero. El cero ya no se sustituye porque al operar con él da cero. Por tanto dos al cubo partido tres es la solución del área comprendida bajo la parábola hasta el eje x tomando como límite derecho la recta vertical que pasa por el punto dos.
-------------------------------------------------------------
Se trata de calcular el área de la zona amarilla, la que define la curva de color rojo y cuya ecuación vemos en la parte inferior izquierda. Vamos a calcular el área de la zona azul, luego se la restamos al cuadrado comprendido entre el cero y el uno, obteniendo así la mitad del área de la zona amarilla, que multiplicaremos por dos para tener el área total: 0,8 × 2 igual a 1,6.
Si calculamos la integral desde uno hasta cero de la ecuación dada en color rojo, habrá que sumarle una unidad al exponente y ese mismo número ponerlo de denominador, tal y como aparece arriba en color verde. Al calcular la integral tenemos el área desde la curva hasta el eje x.
Luego sustituimos la unidad dentro de la variable x y obtenemos que el área desde la curva hasta el eje x vale 0,2, con el signo negativo, cuestión irrelevante para el área - ya no restamos al sustituir el cero, pues estando éste de denominador sale cero.
Como ya dijimos antes el área del cuadrado del cuarto cuadrante se obtiene multiplicando el lado al cuadrado, 1 × 1 es igual a uno menos el área antes calculada, que es 0,2 tenemos que la franja amarilla derecha tiene por área 0,8 unidades, que multiplicada por dos -que la parte del izquierdo es su simétrica- obtenemos el área total de la franja amarilla.
--------------------------------------------------------------------
Ejercicio análogo al anterior.
Se pide calcular el área comprendida entre los elementos determinados por las tres ecuaciones encerradas en un rectángulo rojo
Los tres elementos son: La ecuación de la curva cúbica en color verde y la recta vertical coincidente con el eje Y ( x igual a 0) y la horizontal de coordenada menos 3 (y igual a menos 3)
Primero calculamos la intersección de la curva cúbica dada, igual a -3 x al cubo, con la recta y= -3.
La resolución de ambas ecuaciones aparece en el rectángulo azul en la que obtenemos el punto de coordenadas (1 ,- 3)
Una vez que ya sabemos que esa recta corta en el punto de coordenada en X igual a 1, ya sabemos que la integral está evaluada entre 0 y 1.
Al calcular la integral de la función obtendremos el área comprendida entre los dos segmentos naranjas horizontal y vertical y la curva verde dada, cuyo valor es 0,75 negativo por estar bajo el eje x.
Como el área del rectángulo es 1 por 3 o sea 3, tendremos que restar a 3 el valor del área anterior, -0,75, sin tener en cuenta su valor negativo
3-0,75=2,24 tenemos que el área de la zona rosa vale 2,24
--------------------------------------------------------------------
Tenemos la ecuación de la curva cúbica y queremos obtener el área de la franja amarilla, hacemos la integral de la misma comprendida entre el origen 0 y el punto -1, de esta manera obtenemos el área bajo la curva entre esos dos punts del eje x.
Sumamos una unidad al exponente de x y ese mismo número lo ponemos en el denominador. Luego sustituimos el 0 y el -1 aplicando la diferencia entre ambos, de esta forma obtenemos menos -3/4, esto es 0,75.
--------------------------------------------------------------------
En la figura podemos ver dos curvas, una parábola cuya ecuación aparece en color rojo y una cúbica, cuya ecuación aparece en color azul. Para calcular el área comprendida entre ambas en el primer cuadrante, aplicamos la integral de la segunda expresión o miembro de la ecuación cuadrática menos la segunda expresión de la ecuación cúbica, esto es x al cuadrado menos x al cubo partido por tres.
Calculamos la intersección de ambas ecuaciones y obtenemos como puntos de intersección (0,3). Eso quiere decir que la integral la vamos a evaluar entre tres y cero.
Para calcular la integral sumamos una unidad a cada exponente y ese mismo número lo tomamos como denominador, x al cuadrado se transforma en x al cubo partido por tres, menos x al cubo partido tres que se transforma en x a la cuarta partido por 3 × 4.
Como la integral está evaluada entre el punto tres y el cero, sólo sustituimos en la nueva expresión el valor tres, ya que si le restamos a la misma expresión pero sustituyendo el valor cero en la variable x, obtenemos también cero. Por tanto al sustituir el tres en la variable x obtenemos 2,25 unidades cuadradas, que es el área comprendida entre las dos curvas y que en el dibujo aparece en color naranja.
-------------------------------------------------------------
En una integral indefinida, en este caso determinada por una parábola, si calculamos el valor de la integral y lo sustituimos por un número, por ejemplo el número dos, tenemos que el valor que vamos a obtener corresponde al área comprendida entre ese número que corresponde a la vertical x=2 y la vertical x=0, por debajo de la curva y hasta el eje x. Siempre se va a calcular el área por debajo de la curva hasta el eje x entre el número escogido y entre el cero (x=0).
Calculamos el valor de la integral sumando una unidad al exponente y tomando el nuevo valor del exponente también como denominador: 2x al cuadrado se transforma en 2x al cubo partido tres, mientras que 3x elevado a cero -o lo que es lo mismo 3- le sumamos una unidad a x y obtenemos 3x partido por uno. Sumamos este término al anterior y le agregamos la suma de una constante cualquiera aleatoria c.
Sustituimos a continuación el punto dos en la función en la variable independiente x obteniendo el valor 11,33, esto quiere decir que ésta es el área de la región amarilla entre el dos y el cero, de esta manera la integral pasa de ser indefinida, que quiere decir que no están establecidos el límite máximo y mínimo o los intervalos entre los que vamos a calcular el área a concretar a ser definida entre 2 y 0.
---------------------------------
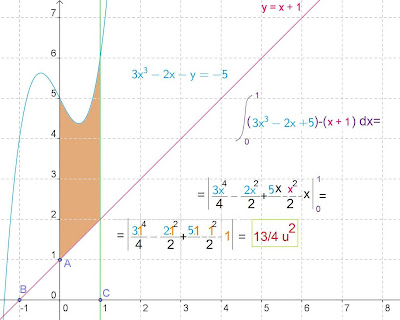
En la figura tenemos una parábola y una recta, vamos a calcular el área comprendida entre ambas. Resolvemos la intersección entre ambos elementos, para ello resolvemos el sistema de ecuaciones correspondientes a la curva y a la recta y de esta forma tenemos que se cortan en los puntos: (1,1) (0,3). Por tanto la integral estará definida por los valores de x de ambos puntos, esto es, entre uno y cero. Aplicamos entre ambos valores la integral de la diferencia de la expresión de la curva menos la de la recta.
Incrementando una unidad al exponente de cada variable y considerando este número en el denominador y a continuación sustituyendo el uno en la variable obtendremos el área de la franja amarilla, que es un tercio.
-------------------------------
En la figura tenemos 2 parábolas, vamos a calcular el área comprendida entre ambas. Resolvemos la intersección entre ambos elementos, para ello resolvemos el sistema de ecuaciones correspondientes y de esta forma tenemos que se cortan en los puntos: (1,1) (-1,1) Por tanto la integral estará definida por los valores de x de ambos puntos, esto es, entre 1 y -1. Aplicamos entre ambos valores la integral de la diferencia de la expresión de la curva superior menos la inferior.
Incrementando una unidad al exponente de cada variable y considerando este número en el denominador y a continuación sustituyendo el uno y menos uno en la variable obtendremos el área de la franja amarilla, que es 4.
---------------------------------------------------
En la figura tenemos la ecuación de la parábola de la que queremos calcular el área comprendida entre el segmento vertical que pasa por el punto uno y por el eje x.
Aplicamos la integral en el límite superior 1, sustituyéndolo en la nueva expresión. Como sabemos, en la variable independiente x tenemos un exponente al que le añadimos una unidad y este nuevo número obtenido lo ponemos además en el denominador, por tanto -2x al cuadrado se transforma al integrarlo en -2x al cubo partido por tres.
Hacemos lo mismo con el segundo término y evaluamos la expresión en el punto uno, que quiere decir que sustituimos el uno en la x. Con el cero ya no es necesario hacerlo porque el resultado va a ser cero.
Al sustituir el uno obtenemos que el área en color amarillo vale 0,83 unidades cuadradas.
------------------------------------------------------------
Tenemos la función cúbica en el rectángulo amarillo de la parte superior. se trata de hacer el área comprendida entre la curva y el eje x, esto es la ecuación y = 0.
Sumamos en cada una de las variables de los términos una unidad a los exponentes
(x al cubo pasa a ser a la cuarta) y ese mismo número lo ponemos en los denominadores
correspondientes (rectángulo naranja inferior).
(x al cubo pasa a ser a la cuarta) y ese mismo número lo ponemos en los denominadores
correspondientes (rectángulo naranja inferior).
Una vez calculada la integral (rectángulo naranja inferior) sustituimos el valor desde 2 hasta 0 que son los puntos de intersección de la curva con el eje dado (prescindimos de sustituir el 0 pues da 0).
De esta manera obtenemos el valor absoluto del área, que es 1,33 ya que por estar debajo del eje x
sale con signo negativo.
sale con signo negativo.
Para representar la curva hacemos la derivada (rectángulo gris) y la igualamos a cero, de esta manera podemos observar dónde están los puntos críticos en x, esto es: 1,33 y 0 (máximo y mínimo), para saber si por ejemplo el mínimo era el punto de la derecha, calculamos la derivada en el punto 2 de la curva y vimos que la pendiente de la tangente es positiva y por tanto es una línea reciente y quiere decir que efectivamente en ese punto teníamos un mínimo ya que luego la curva sube hacia la derecha.
Cuando una función pasa por debajo del eje x, su área hasta x va a ser negativo en la integral, de ahí que cojamos el valor absoluto, 1,33 en este caso.
-----------------------------------------------------------------------
Para calcular el área comprendida entre la parábola y el eje x entre los límites de integración 1 y -1, que corresponden a los extremos verticales de la figura del que se va a calcular el área, hacemos la integral de la ecuación de la curva evaluado entre 1 y -1. Podríamos hacerlo sustituyendo sólo el uno, y el valor obtenido correspondiente al área de la figura sería desde el uno hasta el cero, a continuación multiplicaríamos por dos esta área.
En la figura se ha calculado la distancia focal, para ver su cálculo observar el apartado en este blog sobre la parábola.
-----------------------------------------------------------------------------
En la figura tenemos una parábola cuya ecuación aparece en color verde y una recta bisectriz de los ejes cartesianos, la correspondiente al primer cuadrante.
Para calcular el área bajo la curva hasta la recta calculamos la intersección de ambos elementos y obtenemos el primer punto a la derecha que es cero, mientras que a la izquierda el segundo punto de intersección es C, de coordenadas (-0,5, -0,5).
Hacemos la integral por tanto de la ecuación de la curva menos la ecuación de la recta, comprendido entre los puntos correspondientes al eje x, que son 0 y -0,5.
Al calcular la integral sabemos que tenemos que sumar una unidad al exponente y tomar ese mismo número también como denominador, sustituyendo a continuación el cero, nos da cero menos la misma expresión sustituyendo el -0,5, obtenemos el valor del área 0,041
----------------------------------------------------------------------------------
Para calcular el área en color amarillo comprendida entre la parábola y la recta de ecuación y=4, calculamos la intersección de ambos elementos, teniendo el 2 y el -2 como puntos de intersección correspondientes al eje x.
Calculamos la integral de la curva menos la recta evaluadas ambas entre 2 y -2. Sustituyendo ambos números al calcular la integral obtenemos 10,6 unidades cuadradas.
------------------------------------------------------------------------------
Para calcular el área comprendida entre la recta de ecuación y=3x (recta que tiene de pendiente tres unidades y que pasa por el origen de coordenadas) y la curva parabólica y = x al cuadrado, comprendida entre el dos y el cero, calculamos la integral de la línea menos la curva sustituyendo al hacer el cálculo el punto dos en la variable x.
en el dibujo se sustituye también la segunda parte, el cero en la variable x obteniendo como resultado cero, por tanto no es necesario sustituirlo.
-----------------------------------------------------
En la figura tenemos una parábola en color violeta y su correspondiente ecuación, se pide calcular el área comprendida entre su intersección con el eje x por la derecha hasta el origen de coordenadas, esto es, la franja pintada de color azul.
Simplemente aplicamos la integral de la ecuación y a cada uno de los dos términos le sumamos una unidad al exponente y ese mismo número lo consideramos también como el numerador. A continuación, en color verde, mostramos una expresión en la que hemos sacado factor común.
Para calcular la intersección de la curva con el eje x, debemos saber que la ecuación de ese eje es y=0, sustituyendo en la ecuación original de la curva obtenemos el valor de x, que es 1,4. Sustituimos este número en la ecuación de color verde dentro de la variable x y obtenemos que el valor del área es 1,8.
-----------------------------------------------------------------
En la figura tenemos en el rectángulo verde de la ecuación de una parábola de la que se pide el área comprendida entre el punto dos del eje x y el punto D de coordenadas (1,41, 0). Se pide además calcular la pendiente de la recta tangente en el punto B.
Hacemos la integral de la función, elevamos una unidad al exponente de x en ambos términos, y ese número obtenido lo utilizamos como denominador.
2 se transforma en x, ya que 2x0 se transforma en e 2x0+1 /1
Si sustituimos el dos en la variable x obtenemos -1,3. Como el área verde, al calcular la integral por estar encima del eje x su valor sale positivo mientras que el área de la franja amarilla por estar debajo sale negativo, el resultado de calcular el área al sustituir el número dos en la integral es la resta de ambas: 0,5-1,87=-1,3, ya que al calcular la integral definida en el punto dos, se obtiene el área comprendida entre este punto y el cero, mientras que al calcular el área comprendida entre el número 1,41, se obtiene el área comprendida entre este número y el cero, por tanto la primera área menos la segunda área nos da el área verde, teniendo en cuenta que cuando calculemos el área de la franja amarilla sale negativo.
Para calcular la pendiente de la recta tangente hacemos la derivada de la función, en cada término se multiplica el exponente por la función restándole luego una unidad al exponente, así, x2 se transforma en 2x y el segundo término -2 se transforma en cero. obtenemos la nueva función y=2x en la que sustituimos 2 en la coordenada en x, ya que ésta es la coordenada del punto dado B.
y=2.2= 4, en consecuencia cuatro es la pendiente de la recta tangente en ese punto a la curva, que quiere decir que si por ese punto hacemos una línea horizontal hacia la derecha de valor una unidad y por el extremo levantamos una vertical que corta a la recta tangente en un punto, al unirlo con el extremo anterior, se obtiene una dimensión de cuatro unidades.
----------------------------------------------------
En la figura observamos una parábola y su ecuación en el borde superior derecho, en color azul y rojo. Vamos a calcular el área por debajo de la curva hasta el eje x. Calculamos la intersección de la curva con el eje x, para ello sabemos que la ecuación de este eje es y=0, por tanto sustituyendo el cero en la ecuación original de la curva, tenemos que los puntos de intersección obtenidos son el 2 y el -2. Aplicando la integral -x elevado al cuadrado mas cuatro, tenemos -x elevado al cubo más 4x, después de añadirle una unidad al exponente y tomar el valor del exponente también como denominador.
Como calculamos el área evaluado entre el punto 2 y -2, sustituimos el primer punto en esa expresión y le restamos la misma expresión sustituyendo el -2, obteniendo como área de esa franja rosada 10,66. Para calcular el área de la zona verde basta con calcular el área del rectángulo que es 4 × 2 igual a 8, restando de esta cantidad la mitad de la anterior, esto es 5,33, obtenemos el área de la zona verde que es 2,67.
En la zona de la izquierda, hemos calculado el vértice y la distancia focal de la curva, despejamos la variable x dejándola sola a la izquierda -la que tiene el exponente elevado al cuadrado- y sacamos factor común a -y+4, de esta manera tenemos que -1 multiplica a y-4. Por tanto el foco tiene por coordenadas (0,4), el primer número corresponde a x-0 (elevado al cuadrado), expresión del primer término a la izquierda, mientras que la variable y corresponde a y-4.
Hemos sacado factor común y tenemos que -1 multiplica a la expresión anterior, esto quiere decir que 4p es igual a -1 por tanto p es igual a -0,25. Si restamos a cuatro esta medida obtenemos como valor absoluto 3,75, por tanto las coordenadas del foco son (cero, 3,75). Para comprender de dónde sale todo esto se recomienda observar en este mismo blog el apartado sobre la parábola.
------------------------------------------------------------------------------------
En la figura vamos a calcular el área coloreada en un tono verde, franja de intersección de las curvas de segundo y tercer grado. Vamos a calcular la integral en función de y. Para ello despejamos la x y tenemos las dos expresiones del borde superior derecho.
Resolvemos el sistema de ecuaciones y tenemos que la intersección de ambas curvas es 1 y -1 punto por tanto vamos a evaluar el área entre estos dos puntos.
Calculamos la integral de la parábola roja menos la de la curva azul sumando una unidad al exponente de cada variable y considerando ese número como nuevo denominador, después de restar una menos la otra sustituimos el 1 y a continuación el -1 en la variable y en toda la expresión, obteniendo como área 4/3.
-----------------------------------------------------------------
En la figura tenemos dos parábolas, la parábola de color magenta y la de color verde, aplicando la integral de la primera menos la segunda obtenemos el área de la zona amarilla. Calculamos la intersección de ambas curvas, para ello resolvemos la solución al sistema de ecuaciones de ambas curvas obteniendo dos y cero.
Calculamos lo integral entre estos dos puntos y de esta forma obtenemos el área de la franja amarilla que es 2,6 unidades cuadradas.
---------------------------------------------------
En la figura se muestra el cálculo del área bajo la curva hasta el eje x mediante una integral evaluada entre 4 y -4. Para calcular la integral sumamos una unidad al exponente de cada variable y consideramos ese número también como nuevo denominador, a continuación sustituimos el cuatro en esa expresión y le restamos a continuación la misma expresión sustituyendo también el -4. Obtenemos de esta manera el área que es 26,67 unidades cuadradas.
---------------------------------------------
En la figura tenemos una recta y una parábola, para determinar el área entre ambas curvas comprendida entre el intervalo 2 y 1, aplicamos la integral de la primera función menos la segunda.
Debemos graficar ambas funciones para verificar si efectivamente están por encima del eje x, en caso de que no fuera así tomaríamos el valor absoluto de lo que aparece por debajo del eje x. como podemos ver en el dibujo el punto uno en x es realmente un punto de intersección de ambos elementos.
En color verde aparece la primera expresión a la que se resta en color rojo la que corresponde a la parábola.
Como ya sabemos, para integrar sumamos una unidad al exponente de la variable x en cada término y este mismo número lo ponemos en el denominador. Una vez que operamos sustituimos en toda la expresión el dos en la variable x y a continuación repetimos la misma expresión y sustituimos el uno en la misma variable, obteniendo como resultado 2,17 unidades cuadradas.
Para calcular el área comprendida entre la curva azul de tercer grado y la recta magenta, comprendida entre el uno y el cero, despejamos y en las dos ecuaciones y obtenemos los elementos que aparecen en la integral en el borde superior derecho, aplicando la diferencia de ambos y aplicando la integral entre el uno y el cero, obtenemos el área de la franja siena.
Para calcular la integral sumamos una unidad al exponente y consideramos también ese nuevo número como el denominador, en la variable x sustituimos sólo el uno, ya que si le restamos a la misma expresión sustituyendo en x el valor cero tenemos también 0, y algo menos cero es lo mismo, por eso ya no lo hacemos.
--------------------------------------------------------------
En la figura tenemos una curva y igual a nueve que multiplica a x elevado a tres medios, que es lo mismo que nueve que multiplica a raíz cuadrada de x al cubo.
Calculamos el área bajo la curva comprendida en el intervalo uno y 0, para ello calculamos la integral definida de la curva entre ambos puntos, sumamos una unidad al exponente de la variable y consideramos también este nuevo número como denominador.
Una vez que hemos calculado la integral, sustituimos el uno en esa expresión y volvemos a repetir la expresión sustituyendo el cero, aplicando la diferencia de ambas, obtenemos de esta manera que el valor del área comprendida bajo la curva es es 3,6.
Para calcular el área de la franja amarilla obtenemos el área del rectángulo que es suma de las 2 áreas, multiplicando la base por la altura, esto es 9 × 1 tenemos que es igual a nueve. Restando a este número el valor del área anterior, 3,6, obtenemos el valor del área de la franja amarilla, 9 - 3,6 igual a 5,4.
------------------------------------------------------------
En la figura tenemos en color ocre la ecuación de una curva de la que vamos a calcular el área comprendida entre los puntos de intersección con el eje x.
Sabemos que la ecuación de este eje es y=0, en consecuencia calculamos el valor de x, que es 0 y 1. Aplicamos la integral de la expresión de la curva evaluada entre esos dos límites. Para calcular la integral elevamos una unidad al exponente y consideramos también ese nuevo número como denominador, la expresión obtenida la repetimos dos veces, aplicando la diferencia de la primera menos la segunda y sustituyendo en la primera el valor de uno y en la segunda el valor de cero, al hacer el cálculo obtenemos el valor absoluto 0,3, número que sale negativo por estar debajo del eje x.
----------------------------------------------------------
----------------------------------------------------------------
Si queremos calcular el área comprendida entre la curva y el eje x desde uno hasta cero, tomamos la ecuación de la curva y la integramos: la raíz de x es x elevado a un medio, al integrar esta expresión tenemos que sumarle una unidad por lo que queda x elevado a tres medios y dividido todo entre tres medios. Multiplicando medios y extremos el denominador del denominador pasa al numerador y por tanto obtenemos 2/3 de raíz de x elevado al cubo (que es lo mismo que x elevado a tres medios). Sustituyendo en esta variable el punto uno tenemos el valor del área de color verde que es 0,66 unidades cuadradas.
----------------------------------------------
Si queremos calcular el área comprendida entre la recta de ecuación y =1 y la parábola de ecuación y igual a raíz cuadrada de x, estamos el segundo miembro de la primera ecuación menos el segundo miembro de la segunda. Hay que calcular la integral definida de esa expresión o diferencia de ambas curvas entre la intersección entre ambas y el cero. Si sustituimos el valor de la primera ecuación en la segunda, tenemos que cuando y vale uno, x vale también uno, este es un punto de intersección de ambas.
Calculando la integral de la expresión y evaluando la sustituyendo el uno en la variable x, obtenemos que el área es 0,33.
---------------------------------------------------
Tenemos la ecuación de la cúbica en color rojo y La ecuación de la parábola en color verde y vamos a calcular el área comprendida entre ambas curvas y la recta vertical que pasa por x=1.
Como la curva roja está por encima de la verde en esa franja -Desde el uno hasta el cero- hacemos la diferencia de estas y aplicamos la integral entre uno y cero. Sumamos una unidad a cada incógnita x y ese mismo número lo ponemos de denominador, sustituimos luego el uno en esa incógnita y resolvemos el quebrado, obteniendo 2,916.
Como podemos ver hemos sustituido el uno en la variable pero no hemos sustituido el cero ya que nos daría cero directamente.
---------------------------------------------------
---------------------------------------------------
Tenemos la ecuación de la cúbica en color rojo y La ecuación de la parábola en color verde y vamos a calcular el área comprendida entre ambas curvas y la recta vertical que pasa por x=1.
Como la curva roja está por encima de la verde en esa franja -Desde el uno hasta el cero- hacemos la diferencia de estas y aplicamos la integral entre uno y cero. Sumamos una unidad a cada incógnita x y ese mismo número lo ponemos de denominador, sustituimos luego el uno en esa incógnita y resolvemos el quebrado, obteniendo 2,916.
Como podemos ver hemos sustituido el uno en la variable pero no hemos sustituido el cero ya que nos daría cero directamente.
---------------------------------------------------
Para calcular el área bajo la curva entre el intervalo 0 y -1, en cada término que integramos de la función elevamos una unidad al exponente y lo dividimos por el mismo número, a continuación sustituimos el cero en la variable de la expresión y le restamos a la misma expresión sustituyendo esta vez el -1 en x.
De esta forma obtenemos que el área bajo la curva entre ambos puntos es 0,14 unidades cuadradas.
----------------------------------------------
En la figura vemos la función coseno en color verde, una curva con forma de sinusoide que oscila en sus puntos máximos y mínimos entre el 1 y el -1, respectivamente. Para calcular el área comprendida entre cero y dos pi (la circunferencia completa), representamos la curva y observamos que el coseno de 0 es 1, por tanto es un máximo a la izquierda del dibujo, sobre el eje cartesiano de las ordenadas.
A continuación representamos el coseno de 90° (o bien de pi/2 si lo hacemos en radianes) y marcamos por lo tanto su valor que es cero.
Cuando tenemos 180 ° (o también pi radianes), tenemos que el coseno es -1, por tanto la curva tendrá un mínimo en -1 por pi. A partir de aquí la curva es simétrica respecto a un eje vertical que pase por pi.
Tres medios de pi (o 270°) tiene también un coseno cuyo valor es cero, mientras que por 360° (o 2pi radianes) el valor del coseno es uno.
Tenemos ya representada gráficamente la función por lo que habrá que evaluar la misma entre los intervalos 2pi y cero. Como podemos observar entre 270° y 90° la curva genera 1 área negativa por estar debajo del eje x, por tanto a la hora de hacer la integral de los tres tramos, en el tramo intermedio intercambiamos el límite superior y el límite inferior en donde vamos a evaluar la función (en la expresión integral aparece con dos estrellas, una roja y otra azul), esto sería lo mismo que considerar el valor absoluto del área hallada en esa zona, ya que va a salir negativa siempre por debajo del eje x.
Sabemos que la integral del coseno es el seno ya que la derivada del seno es el coseno, por tanto aplicando el seno de los ángulos que determinan los intervalos de integración tenemos 1 área de cuatro unidades cuadradas.
--------------------------------------------------------------------
En la figura tenemos una ecuación racional en el rectángulo rojo y vamos a calcular su área entre los límites 4 y 1. Para calcular el área bajo la curva hasta el eje x aplicamos la integral.
Como novedad respecto a las integrales anteriores, tenemos que la integral de 1/x es el logaritmo neperiano de x. Al evaluar la nueva expresión entre ambos límites, 4 y 1, sustituimos el primero en la expresión y ponemos en la calculadora logaritmo en base e de cuatro, obteniendo 1,38. Al restar la misma expresión sustituyendo el otro valor, uno, tenemos que el logaritmo en base e de uno es cero, ya que cualquier número elevado a cero es uno. Operando tenemos 8,8 unidades cuadradas de área.
En la figura tenemos una ecuación cúbica en color verde, al aplicar la integral a la misma tenemos la curva de color rojo cuya función aparece en la parte superior del dibujo. Se ha aplicado el mínimo común múltiplo y sacado factor común a la variable independiente en el numerador para obtener la expresión anterior.
Como podemos observar en el dibujo, la curva verde corta al eje x en un punto por el que pasa la vertical azul discontinua que intercepta al mínimo de la curva roja. Si hacemos la derivada de la función roja obtenemos la función verde, de ahí esa propiedad referida anteriormente y estudiada en el apartado de cálculo diferencial.

Si sustituimos en la integral el valor dos, estamos calculando el área por debajo de la curva hasta el eje x, todo ello comprendido entre la vertical que pasa por el punto dos, el que hemos elegido, y la vertical que pasa por el origen de coordenadas 0,0. Esto quiere decir que, según vemos en el dibujo, la franja amarilla tiene un área de seis unidades cuadradas. Todo esto sería lo mismo que evaluar la integral entre dos y cero.
--------------------------------------------------------------------
En la figura tenemos una parábola cuya ecuación aparece en color rojo, para determinar la intersección de la parábola con el eje x, sustituimos y por cero y obtenemos el valor único de x, que es 1,5.
Si sustituimos este valor en la integral de la ecuación dada que es la que aparece en color verde en el borde superior derecho, obtenemos 4,55, que es el área por debajo de la curva hasta ese punto y hasta el punto 0,0 u origen de coordenadas.
En el cuadro azul tenemos la función anterior convertida en un binomio al cuadrado que multiplica a la derivada de la misma, como no es éste el caso ya que la expresión o función dada no contiene a su derivada, multiplicamos por la constante 1 dividido entre la derivada, con esta operación inversa que deja inalterable la expresión podemos aplicar el método que hacemos siempre con la variable x pero esta vez toda la función, a saber, elevamos una unidad al exponente y este número lo ponemos también de denominador, además esta expresión multiplica a uno dividido entre la derivada de lo que aparece dentro del paréntesis. El resultado de hacer todo esto será el mismo que el que corresponde al caso anterior.
---------------------------------------------------------------------------------------------
Volúmenes de figuras
Volumen del cono
Para calcular el volumen de un cono (engendrado por un triángulo de color naranja que gira en torno al eje x) debemos considerar el volumen de los discos o cilindros ortogonales al eje x que tienen por área de la base pi por el radio al cuadrado, y altura dx.
Integrando esa expresión tenemos que el radio de los discos que definen el cono quedan definidos por la ecuación de la recta y=x/2. Sustituimos por tanto x/2 en donde pone R y aplicamos la integral de esta expresión desde el punto cuatro hasta el punto cero, que corresponde a la altura del cono o extremos del eje de revolución por donde va a girar el triángulo naranja.
Aplicando el cuadrado a x/2 tenemos x al cuadrado partido cuatro.
Calculando la integral de esta expresión tenemos que x, al sumarle una unidad al exponente se transforma en x elevado al cubo dividido entre tres.
Al sustituir el valor cuatro en donde tenemos la variable x se define el volumen de la figura.
Como los límites de integración son el cuatro y el cero, tendríamos que sustituir en la variable primero el cuatro y a continuación restarle la misma expresión sustituyendo el cero, pero como en la segunda expresión su resultado es cero, por eso ya no lo hacemos.
Representación volumétrica del cono al girar el triángulo naranja en torno al eje x
--------------------------------------------------------------------------------------------------
Volumen de la esfera
Tenemos la ecuación de la circunferencia que aparece en el borde superior izquierdo en color magenta. Como en la ecuación de la circunferencia el radio al cuadrado es igual a nueve tenemos que el radio de la circunferencia vale tres.
Despejando en la ecuación tenemos que y es igual a la raíz cuadrada de nueve menos x al cuadrado.
Sustituyendo en la integral definida desde el punto 3 hasta el punto -3, (intervalo correspondiente a los extremos del diámetro), tenemos que pi por el radio el cuadrado (el radio de los discos de revolución que giran en torno al eje x y que queda definido por el segundo miembro de la ecuación de la curva, raíz cuadrada de nueve menos x al cuadrado), todo ello al cuadrado por la altura dx de cada cilindro, define el volumen de la curva.
Al aplicar la integral a esa expresión tenemos en el primer término pi por nueve, como el resultado es una constante su integral es x (como multiplica a uno o x elevado a cero, al sumar una unidad al exponente cero tenemos x elevado a uno, o lo que es lo mismo, x, y esta variable dividida entre el exponente uno, obteniendo como resultado final x; sustituimos en esta expresión el 3 y a continuación en la misma expresión sustituimos el -3, por ser éstos los límites de integración.
A continuación hacemos el cálculo integral correspondiente al segundo término pi por x al cuadrado, que se transforma en pi por x al cubo partido entre tres, tras sumarle una unidad al exponente y bajar este mismo número al denominador. hacemos la diferencia al sustituir tres positivo en el primer término y tres negativo en el segundo. El conjunto de estas operaciones definen el volumen de la esfera, cuyo valor es 36 pi.
Podemos comprobar que el resultado es certero, ya que el volumen de la misma queda definido por la fórmula del extremo superior derecho, volumen de la esfera igual a 4/3 de pi por el radio al cubo.
----------------------------------------------------------------------------------------------
Volumen de un elipsoide mediante discos
Obramos con este elipsoide igual que en los dos casos anteriores, el elipsoide se engendra por una semielipse que gira en torno al eje x.
Tenemos que los semidiámetros de la elipse valen 3 y 2 respectivamente.
La ecuación de la elipse queda definida por la expresión central superior, donde a es el semieje mayor tres y b es el semieje menor dos.
Al despejar tenemos que y es la raíz cuadrada de b al cuadrado que multiplica a uno menos x al cuadrado dividido entre a al cuadrado.
Esta expresión es la que deberemos sustituir en la integral de pi por el radio al cuadrado, ya que el diferencial de volumen de un disco es pi por el radio por la altura, siendo ésta dx y la suma de los discos nos da el volumen total.
Al sustituirlo en la R, tenemos que como el radio es al cuadrado y la expresión es una raíz, raíz y cuadrado se anulan, por tanto tenemos la integral (suma de todos los volúmenes) de pi que multiplica a todo lo expresado anteriormente, por dx.
En el dibujo se ha hecho una sección AA para indicar por donde pasaría un cilindro aleatorio -de volumen infinitamente pequeño- de altura dx y cuyo radio quedaría determinado por la ecuación de la elipse, de ahí que se sustituya en R la expresión antes mencionada.
La integral va a estar definida entre el límite 3 y el límite -3, ya que esta longitud total corresponde a los dos extremos del eje mayor.
Para ver cómo se resuelve la integral, podemos ver los dos ejemplos anteriores.
Más ejemplos de cálculo de áreas y volúmenes en el apartado:
Vídeos de áreas y volúmenes por cálculo integral:













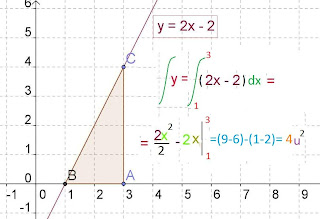








































No hay comentarios:
Publicar un comentario