podemos ver en sus ecuaciones que los términos A y B están invertidos y uno cualquiera de los dos es de signo contrario, como se espera en todo par de rectas perpendiculares entre sí:
Ax+By+C=0 y -Bx+Ay+C=0
0,13x + 0,19y=1 y -0,19x + 0,13y= -0 22
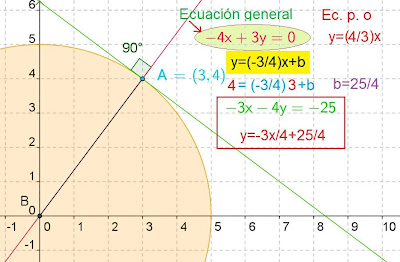
Si tenemos una circunferencia cuyo centro está en el origen de coordenadas, tenemos que toda recta que pasa por el centro es un diámetro normal a la curva. Esta recta perpendicular a la curva tiene por ecuación:
y = pendiente. x+0, como sabemos el coeficiente 0 es el punto de intersección de la recta con el eje y, por tanto es cero, mientras que la pendiente viene determinada por las coordenadas de un punto, por ejemplo el punto A, con tres unidades hacia la derecha su el eje x y unidades hacia arriba a la derecha sobre el eje y, decimos que sus pendiente es de 4/3 (la coordenada en y dividido por la coordenada en x, positiva por estar dirigida creciente hacia la derecha).
Por tanto la ecuación de la recta normal es y=4/3.
Si queremos calcular la recta tangente ortogonal a la anterior, será una recta que tiene pendiente inversa y de signo contrario, por tanto pendientes será -3/4 (volteamos numerador y denominador y le cambiamos de signo). Para determinar el valor del coeficiente b, sustituimos en la ecuación las coordenadas de un punto conocido, por ejemplo el punto A, de coordenadas (3,4).
Al despejar en la ecuación azul el coeficiente b tenemos que su valor es 25/4, esto quiere decir que la recta tangente a la circunferencia corta al eje y a una altura de 25/4 (seis con dos).
Cálculo de la tangente y de la normal mediante la derivada
Tenemos la circunferencia del dibujo anterior de ecuación x al cuadrado más y al cuadrado igual a 25, y vamos a calcular la normal y la tangente partiendo de la derivada en el mismo punto A.
Si derivamos la ecuación cuadrática de la circunferencia, el exponente pasa a estar en cada uno de los términos delante de la variable y a ésta le restamos una unidad de su exponente, por lo que la derivada de la ecuación es 2x+2y.y'=0
Despejando y' tenemos que es igual a -x/y, tomando el punto A de coordenadas 3,4 tenemos la pendiente de la tangente a la curva en ese punto al sustituir las coordenadas de ese punto en la ecuación y'=-x/y.
En consecuencia la ecuación tiene esa pendiente -3/4 y en ella y=mx+b sustituimos nuevamente las coordenadas del punto para obtener b, igual que hicimos en el ejercicio anterior.
De esta manera hemos obtenido la ecuación de la tangente, que es 3x+4y=25/4 y de la que inmediatamente podemos tener la ecuación de la recta normal o a partir de la anterior intercambiando en los dos primeros términos los coeficientes de x e y, así como variando a uno cualquiera de los dos el signo.
En cuanto al coeficiente b de la recta normal ya sabemos que vale cero por pasar por el origen de coordenadas.
En la figura observamos una parábola en color rosa con su correspondiente ecuación, a la izquierda en el rectángulo rojo tenemos la ecuación ordinaria, lo único que tenemos que hacer es calcular las coordenadas del vértice C. Para ello, tal y como parece en la elipse azul en el borde inferior izquierdo, le damos los valores 0 para x y para el eje y. De esta manera obtenemos los puntos de intersección con ambos ejes cartesianos.
Cuando x vale cero, y vale + y -2, eso quiere decir que la parábola es horizontal. Cuando y vale cero, el valor de x es -4/3, por tanto éste es el vértice de la parábola, ya que los otros puntos (2, -2) eran simétricos respecto al eje x mientras que -4/3 es el valor único sobre el eje x.
Sustituimos en la ecuación ordinaria (rectángulo del borde superior izquierdo de color marrón dentro del color rojo) las coordenadas xy del vértice de la parábola que son respectivamente hk.
Tomando un punto de la parábola, por ejemplo el cuatro en x y sustituyéndolo en la ecuación tenemos que su valor en y es + y -4. Sustituyendo por ejemplo el (4,4) en la expresión anterior y despejando p, que es la distancia focal entre el vértice y el foco de la parábola tenemos que su valor es 0,75.
De esta manera hemos obtenido ya las coordenadas del foco J, contamos 0,75 unidades a la derecha a partir de -4/3, que es la coordenada del vértice en x, de esta manera tenemos las coordenadas del foco (-0,58, 0).
Para obtener la ecuación de la directriz haremos lo mismo en el otro sentido contamos desde el vértice hacia la izquierda, 4/3 + 0,75 y tenemos 2,08, como estamos más hacia izquierda el valor sigue siendo negativo, por tanto la ecuación de la directriz es x= -2,08.
Si calculamos la derivada de la función tal y como aparece en el borde superior derecho (consultar en el apartado de cálculo diferencial para ver el procedimiento) a sustituir en x el valor cuatro, que es en el que queremos calcular la tangente, obtenemos la pendiente de la recta tangente, que es 0,38.
Para obtener su ecuación sustituimos en y= mx+b el mismo punto de coordenadas (4,4) y la pendiente en donde pone m, al despejar la letra b, obtenemos su valor - que es el punto de corte de la recta con el eje vertical y. Por tanto la ecuación de la tangente es la que aparece en el borde inferior en el centro.
Para calcular la normal cogemos la misma expresión y= mx+b y sustituimos el mismo punto de coordenadas (4,4), ya que vamos a calcular la normal por ese punto y le damos a la pendiente m el valor correspondiente, inverso y de signo contrario, ya que es una recta perpendicular a la tangente (ver el apartado de rectas perpendiculares). De esta manera obtenemos la expresión que aparece en el rectángulo del dibujo en el borde inferior a la derecha.
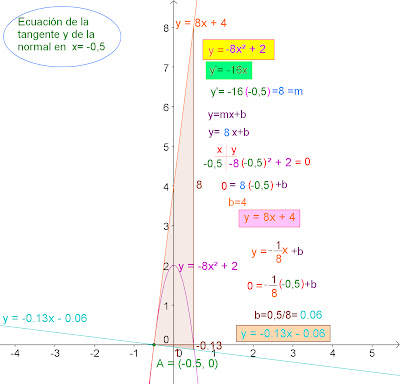
En el dibujo se puede ver una parábola de la que se calculan sus datos (foco, vértice, directriz) en el apartado de este blog acerca de la parábola. Vamos a calcular la recta tangente y normal a la curva en x=-0,5.
Dada la ecuación de la misma, en el rectángulo amarillo, calculamos la derivada multiplicando el exponente 2 por el coeficiente -8 y restándole al exponente una unidad: 2 - 1 igual a 1, a continuación sustituimos 0,5 en la variable x de la derivada obteniendo como resultado ocho, esta es la pendiente de la recta tangente en ese punto (-0,5 , 0). Si queremos calcular la ecuación sustituimos en y=mx+b las coordenadas del punto (-0,5 , 0) por donde pasa la tangente, obteniendo así el valor de la constante b, que es cuatro. La ecuación de la recta tangente es la que aparece en el rectángulo de color rosa.
Utilizamos la misma fórmula para calcular la recta normal, además de tener en cuenta que la pendiente es inversa y de signo contrario. La pendiente de la tangente era ocho, la pendiente de la normal será por tanto -1/8, por ser una recta perpendicular a la anterior. Sustituimos otra vez en y=mx+b el valor de la nueva pendiente -1/8 y en las variables xy el mismo punto y tenemos que b es igual a 0,06, la ecuación de la recta normal es la que aparece en el rectángulo de color carne en el borde inferior derecho.



¿Qué se cumple en la ecuación de una curva?
ResponderEliminar