Recta tangente y normal a una curva
Para calcular la ecuación de la circunferencia dada por dos puntos, el centro de coordenadas (-6, -2) y un punto de la misma de coordenadas (-8,2), además de la recta tangente y normal a la misma, tomamos la fórmula de la ecuación ordinaria de la circunferencia, que es:

Sustituimos en a, b las coordenadas del centro, por lo que tenemos que x menos -6 es igual a x+6, e y menos -2 es igual a y +2. Ambos binomios al cuadrado sumados tienen que ser igual al radio al cuadrado.
Como conocemos un punto de la circunferencia (-8,2), sustituimos las coordenadas de ese punto en la ecuación anterior, de esta manera tenemos que -8 + 6 es igual a -2 al cuadrado es cuatro; más 2 + 2 es 4, que al cuadrado es 16. en total tenemos que la suma de los binomios al cuadrado es igual a 20 (16 + 4), por tanto el radio al cuadrado es igual a 20, así, el radio es la raíz cuadrada de este número, por tanto 4,47.
Si tenemos el radio y tenemos el centro de la circunferencia ya tenemos la ecuación de la misma, que es la que aparece dentro de la circunferencia en color naranja.
La ecuación de la normal que pasa por el punto (-8,2) será la ecuación de la recta calculada mediante la fórmula: y-y2=(y2-y1)(x-x1)/(x2-x1). Sustituimos las coordenadas de los puntos:
y--2=(-2-2)(x--8)/(-6--8), sustituidos de forma indistinta en la fórmula obtenemos la ecuación:
y=-2x-14.
La ecuación de la tangente será una recta perpendicular a la normal por (-8,2), por tanto tendrá una pendiente de 1/2 (-2 cambiado de signo y volteado, ya que dos rectas perpendiculares tienen su pendiente inversa y de signo contrario). Para calcular el coeficiente constante de la ecuación, sustituimos las coordenadas del punto en y=mx+b. 2=(1/2)(-8)+b, despejando b tenemos que su valor es seis, por tanto la ecuación de la recta tangente es y=0,5x+6.
----------------------------------------------------------------------------------------
Un caso particular del anterior es cuando la circunferencia tiene el centro en el origen de coordenadas y cuya ecuación es:
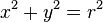 (la misma que antes pero a b valen 0 por estar el centro en el origen)
(la misma que antes pero a b valen 0 por estar el centro en el origen)
Para calcular la recta tangente y normal a la misma en un punto dado A (-3,4), construimos la ecuación de la recta que tiene de pendiente el cociente entre las coordenadas del punto: -4/3. (La pendiente es el cociente entre la coordenada en "y" del punto y la coordenada en x del mismo punto). Como tenemos que la recta pasa por el origen de coordenadas la ecuación queda de la siguiente forma: y=-4/3 x+0, siendo el punto 0 la intersección de la recta con el eje de las ordenadas, cero por estar en el origen.
Ecuación de la recta normal a la circunferencia y que pasa por el punto A y por el origen de coordenadas:
y= -4/3 x ó y= -1,33 x
Para construir la recta tangente o perpendicular a la anterior invertimos la pendiente de la misma y su signo: -4/3 se transforma en 3/4. Para calcular el coeficiente constante del segundo término sustituimos el punto en la forma de la ecuación y=mx+b.
4 = 3/4 (-3) +b, tenemos entonces que b vale 6,25, en consecuencia la ecuación de la recta tangente es:
y= 3/4x +6,25
----------------------------------------------------------------------------------------
Podemos hacer la derivada para calcular la tangente, ya que ésta es la pendiente de la recta tangente en un punto, y si obtenemos la pendiente y tenemos las coordenadas del punto podemos obtener la ecuación de la recta tangente a la curva.
Se trata de calcular la recta tangente a la circunferencia que pasa por el punto C, de coordenada en x=1, para calcular el valor de la coordenada en y, sustituimos en la ecuación el uno en la variable x -esto quiere decir que y vale raíz de 9 - 1= 2,8.
Tenemos la ecuación -en color rojo- de la circunferencia amarilla cuyo centro es el origen de coordenadas.
despejamos la variable "y" y tenemos que es igual a la raíz de nueve menos x al cuadrado.
Si derivamos la ecuación de la circunferencia, tenemos que la derivada del primer término x al cuadrado es dos equis - mirar el apartado de cálculo diferencial de este blog-, la de y al cuadrado es 2y por y', de la que desconocemos su valor. Y la derivada del segundo miembro 9 es cero, por ser una constante.
Si despejamos los elementos de esta nueva expresión hasta dejar la y' sola, tenemos que es igual a -x/y.
Si sustituimos y por su valor, ( raíz de nueve menos x al cuadrado), tenemos ya el valor de la derivada en la que sustituimos el punto 1 -coordenada x- por donde pasa la recta tangente.
Al calcular el valor de y' obtenemos -0,35, que es la pendiente de la recta tangente, su valor negativo indica que su pendiente se eleva hacia la izquierda, si sustituimos en la expresión y = mx+b, siendo m la pendiente y en x,y sustituimos el punto por donde pasa la tangente (1 , 2,8), podemos obtener el valor de b, que es 3,18 -y es el punto donde la recta tangente corta al eje y-, obteniendo de esta forma la ecuación de la tangente: y=0,35x+ 3,18.
------------------------------------------------------------------------------------------
Para calcular las rectas tangentes a una circunferencia (en el dibujo la circunferencia azul de centro en el origen de coordenadas A) desde un punto exterior C, construimos una circunferencia cuyo diámetro sea AC. Para calcular su ecuación debemos obtener el centro y el radio de la misma.
El centro del segmento AC viene dado por la fórmula:
(x1+x2)/2 para calcular la coordenada de x del centro.
Tenemos por tanto que 6 + 0 es igual a seis dividido entre dos obtenemos tres, que es la coordenada en x.
Para calcular la coordenada de y utilizamos la misma fórmula cambiando la variable x por y:
(y1+y2)/2, la coordenada en y es 0 + 0 dividido entre dos que es cero. Por tanto las coordenadas del centro de la circunferencia son (3,0).
(El punto medio entre otros dos se obtiene sumando las coordenadas de ambos y dividiéndolos entre dos, este cálculo se debe hacer sobre las dos coordenadas del punto).
El radio será la distancia desde este punto hasta el punto dado, por tanto es tres unidades sobre x.
Sustituyendo en la ecuación de la circunferencia tenemos el primer binomio al cuadrado con los elementos (x -3) sumado al segundo binomio al cuadrado que es (y -0). La suma de ambos binomios tiene que ser igual a nueve, que es el radio al cuadrado.
Calculamos la intersección de ambas circunferencias que viene dada por la solución al sistema de ecuaciones de ambas circunferencias, de esta manera obtenemos los puntos de intersección EF.
Por último calculamos la ecuación de la recta que pasa por ambos puntos EC mediante la fórmula
y-y2=(y2-y1)(x-x1)/(x2-x1). Hacemos lo mismo con FC o bien cambiamos de signo a los términos del 2º miembro de la ecuación obtenida anteriormente, por ser simétrica respecto a x.
La recta EF se llama recta polar y es aquella que pasa por los puntos de tangencia respecto al polo C desde el que se trazan las tangentes a la circunferencia.
-------------------------------------------------------------------------------
Para calcular la tangente a una curva podemos hacer la derivada de la función. Siendo la ecuación de la curva la igualdad que aparece dentro de la elipse verde, para obtener su derivada multiplicamos el exponente por el coeficiente del término y le restamos una unidad al exponente, con lo que nos queda que la derivada de la curva es: y'=4x
Si tomamos un punto cualquiera de la curva, por ejemplo para x =1, al sustituirlo en la ecuación tenemos que y vale 2. Tenemos por tanto un punto de la curva de coordenadas (1,2). Como la derivada es la pendiente de la recta tangente en un punto, sólo tenemos que sustituir en la variable x de la derivada y'=4x el punto 1, que es el punto por el que queremos calcular la tangente. Tenemos entonces que al multiplicarlo por cuatro obtenemos la pendiente en ese punto, cuyo valor es cuatro.
Podríamos calcular también la ecuación de la recta tangente ya que por tener un punto y la pendiente podemos obtener su ecuación mediante la fórmula pendiente ordenada: y-y2= m (x-x1), siendo m la pendiente - cuyo valor es cuatro- de la recta e x1,y1, las coordenadas del punto que conocemos, en este caso (1,2).
-----------------------------------------------------------------------
x2 = y es la ecuación de una parábola de la que queremos calcular las tangentes en varios puntos. Calculamos la derivada multiplicando el exponente por la variable y restándole una unidad al exponente obtenemos y=2x.
Sustituimos las coordenadas en la variable x de los puntos por donde van a pasarlas tangentes, en 1,2 y 3.
y=2x, sustituyendo tenemos que y=2.1 es 2, y=2.2 es 4 y=2. 3 es 6, éstas son las tres pendientes de las rectas tangentes en esos puntos.
--------------------------------------------------------------------
Para calcular el punto por el que pasa la tangente a una curva paralela a la bisectriz del primer cuadrante, determinamos primero la ecuación de la bisectriz: y=mx+b, como tenemos que la pendiente es la coordenada en y dividido entre la coordenada en x, y como ambas son iguales tenemos que la pendiente es 1 positiva. Tenemos también que b es el punto de intersección de la recta con el eje y, como pasa por el origen de coordenadas b=0. Por tanto la ecuación de la bisectriz del primer cuadrante es y = x.
La ecuación de la parábola es la que aparece en el rectángulo amarillo a la izquierda y = x 2,
Al derivar la ecuación, multiplicamos el exponente por el coeficiente 1 y le restamos una unidad al exponente obteniendo y' =2x
Como la tangente va a ser paralela a la bisectriz, tendrá la misma pendiente que esta, por tanto la tangente tendrá de pendiente una unidad, de esta forma igualamos la derivada a uno. Al despejar x de la nueva ecuación obtenemos que x vale un medio y al sustituir este punto en ecuación de la parábola, obtenemos el valor de y (un cuarto). Por tanto las coordenadas del punto donde la tangente a la curva es paralela a la bisectriz del primer cuadrante son (un medio, un cuarto).
--------------------------------------------------------------------------
Vamos a calcular la tangente y la normal de una curva en un punto dado A, de coordenadas (1, -3).
obtenemos su derivada multiplicando el exponente por el coeficiente 3 y le restamos al exponente de la variable independiente una unidad. Le restamos a continuación la derivada de seis - el segundo término-, siendo ésta cero, por ser una constante. La derivada es y'=6x. Al sustituir la coordenada en x por el punto dado 1, obtenemos la pendiente de la recta tangente, cuyo valor es seis. A continuación en la expresión y=mx+b sustituimos la pendiente y el punto dado, obteniendo el valor de b, que es -9. Por tanto la ecuación de la recta tangente es y=6x-9
Para obtener la ecuación de la recta normal volteamos la pendiente y le cambiamos de signo, por lo que seis se transforma en -1/6. Hacemos el mismo procedimiento para obtener b, sustituimos la pendiente en la ecuación y=mx+b y el punto de la curva en las dos variables xy obteniendo -17/6.
--------------------------------------------------------------------
Tenemos el ejercicio anterior y dada la ecuación de la parábola vamos a determinar su gráfica y distancia focal, así como la directriz.
La ecuación de la curva es la que aparece en la elipse de color verde, graficamos la misma calculando algunos de sus puntos, por ejemplo cuando y es igual a cero, x vale + y -1,4. Por tanto, como ambos puntos equidistan del eje y, tenemos que la parábola va a ser simétrica respecto a este eje vertical.
Si le damos a x el valor de cero, tenemos que el valor de y es -6, eso quiere decir que en el eje correspondiente x, tiene un valor sobre el eje y de -6 unidades, por tanto éste es el vértice de la parábola.
Tomamos la ecuación de la parábola vertical, que es la que aparece en el rectángulo marrón, y sustituimos en h y k las coordenadas del vértice x e y respectivamente.
Si tomamos un punto cualquiera de la curva, por ejemplo le damos en la ecuación a la x el valor uno y obtenemos parar y el valor -3. Tomamos este punto y los sustituimos en la nueva expresión, de esta manera podemos obtener el valor de p. Recordamos que 4p es igual a la distancia focal FV -consultar en esta página el apartado sobre la parábola.
Al despejar la p tenemos su valor 1/12. Ahora podemos sustituir este valor en la ecuación, despejando la y, obtenemos la ecuación original, en consecuencia sabemos que en la expresión x al cuadrado es igual a 1/3 que multiplica (y+6). La directriz será una línea horizontal que quede en el lado opuesto a F y a igual distancia que FV. Siendo la distancia FV 1/12 (o sea 0,08), tenemos que la ecuación de la directriz es y=-6.08.
-------------------------------------------------------------------

Para obtener la tangente de la curva dada en el punto de coordenada x= -1 cuya ecuación es la que aparece en el rectángulo superior, Calculamos la derivada primera obteniendo así la ecuación que aparece en el rectángulo inferior al anterior. Sustituimos el punto -1 en la variable x de la derivada y obtenemos la pendiente cuyo valor es uno (valor de y').
--------------------------------------------------------------------

Si queremos obtener la ecuación de la tangente calculada en ejercicio anterior, hacemos uso de la fórmula en color verde que aparece en el rectángulo amarillo, donde m es la pendiente de la recta e x1,y1 son las coordenadas del punto conocido (-1, -9). Si desconocemos la coordenada en y del punto de la curva, podemos sustituir la coordenada en x en la ecuación dada, de esta manera se puede obtener y, por ser una ecuación con una sola incógnita.
-----------------------------------------------------------------------
Para obtener la tangente y la normal a una circunferencia por un punto de coordenadas (3,4) y cuyo centro de la circunferencia está en el origen de coordenadas, construimos la normal por ese punto, para ello sustituimos en la fórmula y-y2=(y2-y1)(x-x1)/(x2-x1) el punto dado, obteniendo
y-4=(4-0)(x-3)/(3-0)
de esta manera obtenemos que:
y-4=4(x-3)/3, al despejar obtenemos la ecuación general de la normal, que es la que aparece en la elipse verde en el dibujo.
La ecuación tangente en ese mismo punto A por ser perpendicular a la normal tendrá pendiente recíproca y de signo contrario, por tanto la pendiente de la ecuación normal y cuyo valor es 4/3, se transforma en -3/4.
Sustituyéndolo en y=mx+b las pendiente m y el punto dado (3,4), obtenemos el valor de b que es 25/4.
Sustituyendo los datos obtenemos la ecuación de la recta tangente que es la que aparece en el rectángulo rojo inferior.
-------------------------------------------------------------------
o también, y = x 2/4 ó 4y = x 2
Tenemos que la ecuación de una parábola vertical cuyo vértice está en el origen de coordenadas viene dada por la expresión 4p y = x 2, de donde 4p=4, y por tanto p=1, ésta es la distancia focal FV. A continuación podemos dibujarla
Al derivar la parábola queda y = 2x /4, esto es y' = x /2
sustituimos los puntos de coordenada en x, 4, 2,0 en la derivada y obtenemos 2, 1,0, estas son las pendientes de las tangente es en los puntos dados.
----------------------------------------------------------------------
Dada la ecuación de una elipse (la que aparece en la elipse ocre en el borde superior derecho), se pide calcular la tangente en el punto de coordenada en x igual a uno. para obtener la coordenada en y, sustituimos en la ecuación de la elipse el valor 1 en la variable x, al despejar tenemos que el valor de y es 1,88.
La ecuación ordinaria dada de la elipse la transformamos en ecuación general al multiplicar ambos denominadores obteniendo el valor 36 y pasando esta constante el segundo miembro, de esta manera tenemos que esta constante la podemos pasar restando el primer miembro con lo que nos queda
al derivarla tenemos la expresión 18y.y'+8x=0, que, despejando y' tenemos que
y'=8x/18y=-0,24, ésta es la pendiente de la recta tangente en x=1.
----------------------------------------------------------
Dada la ecuación de una hipérbola(la que aparece en la elipse verde en el borde superior derecho), se pide calcular la tangente en el punto de coordenada en x igual a 0,5. para obtener la coordenada en y, sustituimos en la ecuación de la curva el valor 0,5 en la variable x, al despejar tenemos que el valor de y es 2.
Al derivarla tenemos la expresión de la elipse naranja, que, sustituyendo 0,5 tenemos que
la pendiente de la recta tangente en x=-4 (o sea, 4 en vertical y 1 en horizontal). Es el valor de m, en la ecuación verde del rectángulo morado. Sustituimos el valor de x e y y obtenemos b=4, que es donde la recta tangente corta al eje vertical.
----------------------------------------------------------------
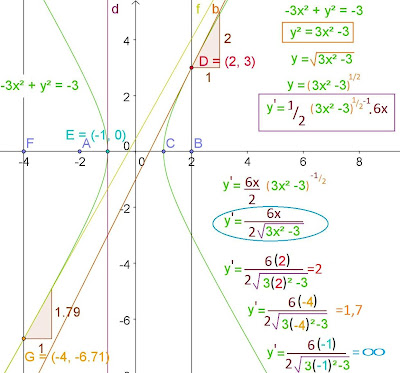
En la figura tenemos una hipérbola dada por la ecuación verde del borde superior derecho, si despejamos y tenemos que y = (3x 2-3)1/2
Esta es otra forma de expresar una raíz cuadrada, elevar el término que está dentro de la raíz cuadrada a un medio.
Al derivarla pasamos el exponente multiplicando a todo el binomio y le restamos al exponente del binomio una unidad, multiplicando a continuación todo lo anterior por la derivada de lo que aparece dentro del exponente, de esta manera obtenemos
y' = [ 1(3x 2-3)1/2.6x] 2
Al sustituir en la derivada varios puntos para obtener las tangentes en ellos, el punto de coordenada en x igual a dos, el punto de coordenada en x igual a -4 y el punto de coordenada en x igual a -1; obtenemos respectivamente las pendientes en esos puntos, que son dos en el primer caso, 1,7 para el segundo caso e infinito para el tercer caso, este último caso es infinito porque la pendiente de una recta vertical es infinita.
------------------------------------------------------------------------
Dada la ecuación de la hipérbola (en color rojo), se pide calcular la tangente o pendiente en el punto cuya coordenada en x es igual a uno. Para obtener la coordenada en y sustituimos el uno en la ecuación dada, de esta manera obtenemos que el valor de y es 1,12.
Derivando la ecuación y pasando las variables y' al primer miembro tras factorizar, tenemos que
y' = (2+6x)/(6y+2).
Al sustituir las coordenadas del punto en las dos variables xy obtenemos la pendiente de la curva cuyo valor es 0,92.
------------------------------------------------------------------
En el dibujo observamos una curva en color azul con su correspondiente ecuación. Se pide calcular el punto en el que una tangente a la misma tenga pendiente cuatro. Para ello calculamos su derivada (función de color marrón) e igualamos el segundo miembro a la pendiente dada, cuatro. Al despejar la variable independiente x obtenemos su valor que es 1, 41 (cálculo en el rectángulo rojo). Sustituyendo en la ecuación original este valor, obtenemos tres para la variable dependiente y. Por tanto en el punto de coordenadas (1,41 , 3) la tangente tiene una pendiente de cuatro unidades.
Se pide calcular también la pendiente de la tangente en el punto de inflexión E, esto es, donde cambia de convexa a cóncava. Para obtener el punto de inflexión de la curva tenemos que construir la segunda derivada, por tanto tomamos la primera y la derivamos, obteniendo y''= 6x. Igualamos el segundo miembro a cero y tenemos que cuando y vale cero, x también vale cero. Esto quiere decir que el punto de inflexión queda en la coordenada x= 0. Para conocer su coordenada en y, sustituimos el cero en la ecuación original de la curva dada (la ecuación azul). Tenemos que el valor de ese punto sobre el eje y, vale tres. Por tanto conocemos el punto por donde tenemos que calcular la tangente y su pendiente, es el punto de coordenadas (3,1).
Para calcular la pendiente de la tangente en este punto necesitamos sustituir la coordenada en x en la primera derivada (cálculo en el rectángulo azul). Al sustituir 0 en x observamos que el valor de y' es -2, por tanto ésta es la pendiente de la tangente en E (3,1).
------------------------------------------------------------
Tenemos una rama parabólica, que es la curva de color rojo en el dibujo, queremos calcular la tangente en dos de sus puntos, si tomamos la ecuación de la curva (en color rojo) y la derivamos -ver procedimiento en el apartado de cálculo diferencial-, obtenemos la ecuación de color azul, sustituyendo en las coordenadas en x de los puntos en los que queremos calcular las tangentes, obtenemos la pendiente de ambas rectas:
Para el punto de coordenadas (-1,1), tenemos que su pendiente vale uno (forma 45° con el eje x). Por tanto la ecuación de la recta tangente será y= x mas la constante 2, que es el punto de intersección de la recta con el eje y. Para calcular la ecuación de la recta utilizamos la ecuación (y-y1)/(x-x1)=(y2-y1)/(x2-x1), siendo el valor del cociente (y2-y1)/(x2-x1) la pendiente de valor igual a 1. (Véase el apartado de incidencia).
Si sustituimos la coordenada en x del punto (3,3), que es el punto tres en la derivada o fórmula de color azul, obtenemos que la pendiente de la recta es un tercio, por tanto sustituyendo en ecuación dada anteriormente obtenemos la ecuación de la tangente que es y=1/3 x+2
-------------------------------------------------------------------
En el dibujo podemos ver una función cuya expresión matemática queda definida dentro de la elipse naranja en la parte superior. Como podemos observar es el producto de un binomio y un trinomio, por tanto para calcular la derivada de esa expresión aplicamos la fórmula que aparece en el rectángulo azul: la derivada de un producto es igual a la derivada del primer término por el segundo término más la derivada del segundo término por el primer término. (Ver apartado de cálculo diferencial en este blog).
Si aplicamos la fórmula, obtenemos la expresión que aparece en el rectángulo violeta, haciendo el producto de sus términos y simplificando obtenemos la expresión que aparece en el rectángulo verde, como queremos calcular la tangente en el punto de coordenada en x igual a uno, sustituimos en la expresión del rectángulo verde el uno en la variable independiente x. De esta manera tenemos que la derivada en ese punto tiene valor 12. Esto quiere decir que la pendiente de la recta tangente en ese punto vale 12 unidades que significa que la recta sube hacia la derecha por ser positiva 12 unidades en vertical por cada unidad en horizontal, tal y como se ve en el dibujo de la recta tangente (en color azul).
Tomando la fórmula de la ecuación punto-pendiente, que aparece debajo del eje x en color negro, y sustituyendo las coordenadas (1,0) del punto A por donde pasa la tangente, -al sustituir en la ecuación original dada el valor de x, en este caso 1, obtuvimos el valor de y, que es cero. Sustituimos en la fórmula el valor de la pendiente m, que en este caso es 12, y obtenemos la ecuación de la tangente que aparece en color azul dentro del rectángulo rojo.
-----------------------------------------------------------
-------------------------------------------------------------------------------------
Cálculo de una recta paralela y tangente a una curva.
Dada una parábola definida por la ecuación que aparece en la elipse, se pide calcular la tangente a la misma y que al mismo tiempo sea paralela a la recta dada y=2x+5.
Despejamos la ecuación de la parábola y dejamos el término de la variable y a la derecha mientras que en el miembro de la izquierda dejamos el término con la variable x y el coeficiente sin variable y cuyo valor es 4.
Tenemos por tanto que 2/3 de x al cuadrado es igual a y -4/3.
Despejando los 2/3 y pasándolos al segundo miembro tenemos que x al cuadrado es igual a tres medios de (y -4/3). Mediante este procedimiento hemos calculado las coordenadas del vértice, como x está sólo en el primer miembro, tenemos que la coordenada en x vale cero, mientras que la coordenada en y vale 4/3 o 1,33. Para ver este detalle consultar el apartado de la parábola en este mismo blog.
Tenemos también que 4p es igual a tres medios, que es lo que aparece en la expresión anterior. Tenemos que p es la distancia focal FV, por tanto al despejar p tenemos que p=3/2.4= 3/8= 0,38. De esta forma podemos representar la curva con precisión para entender mejor el dibujo.
La derivada de la ecuación de la parábola es 4/3 de x. ( Mirar el apartado de cálculo diferencial para obtener derivadas de ecuaciones).
Si sustituimos en esta expresión en y' el 2, pendiente de la recta dada (nº al lado de x), obtenemos el valor de x, que es 1,5. Cogimos el dos porque es la pendiente de la paralela a la que va a ser la recta tangente, esto es, la derivada, y la pendiente de la recta dada vale dos por que ese es el coeficiente que aparece al lado de la variable x.
Sustituyendo ahora el valor de x (1,5) en la ecuación de la parábola tenemos que el valor de y que es 2,83, esto quiere decir que el punto de coordenadas (1,5 , 2,83) es el punto de tangencia por donde pasará la recta tangente a la parábola y que es paralela al mismo tiempo a la recta dada.
y=2x+b nos da la ecuación de la tangente, tiene 0 pendiente que la recta dada. Sustituimos en x y el punto de tangencia: (1.5 ,2.83) y obtenemos el valor de b que es -0,17, por tanto es el punto de corte con el eje y: y=2x-0,17 es la ecuación de la recta.
Una vez que hemos obtenido el punto de tangencia, para calcular la ecuación de la recta tangente, tenemos que toda ecuación de una recta queda definida por la expresión: y = mx+b, siendo m la pendiente de la recta y b la intersección con el eje y. ( Consultar en este blog el apartado de ecuación de una recta)
Sustituimos por tanto en esa expresión la pendiente que vale dos y las coordenadas del punto anterior obtenido (1,5 , 2,83). De esta forma obtenemos el valor de el coeficiente b que es -0,17. Podemos en consecuencia sustituirlo en la expresión y = mx+b y obtenemos de esta forma la ecuación de la recta tangente paralela a la dada, que era lo que se buscaba.
Hemos multiplicado ambos miembros por 1,5 para obtener la expresión que aparece en el rectángulo de extremos redondeados. La recta violeta es la solución.
--------------------------------------------
























buen aporte a la comunidad estudiantil gracias
ResponderEliminarMuchas gracias
EliminarGracias a ti, saludos
ResponderEliminarGracias me sirvio mucho
ResponderEliminarGracias, chao
Eliminarexcelente aporte.. me cayo de diez... consegui resolver un cuestionario que no estaba entendiendo.. gracias
ResponderEliminarGracias, amigo
EliminarBuen aporte
ResponderEliminar